😎 공부하는 징징알파카는 처음이지?
[이것이 코딩 테스트다 with Python]_19_BFS 본문
728x90
반응형
220202 작성
<본 블로그는 『이것이 취업을 위한 코딩 테스트다』 의 youtube를 참고해서 공부하며 작성하였습니다>
https://www.youtube.com/watch?v=CJiF-muKz30&list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81&index=19
1. BFS (Breadth - Frist Search)
: 너비 우선 탐색
: 가까운 노드부터 우선적으로 탐색함
: 큐 자료구조 이용
1) 탐색 시작 노드를 큐에 삽입하고 방문 처리
2) 큐에서 노드를 꺼낸 뒤, 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입 하고 방문 처리!
3) 2번 과정을 수행할 수 없을 때까지 반복
+) 동작 예시
- 시작 노드 1
: 큐에 삽입하고 방문 처리 !
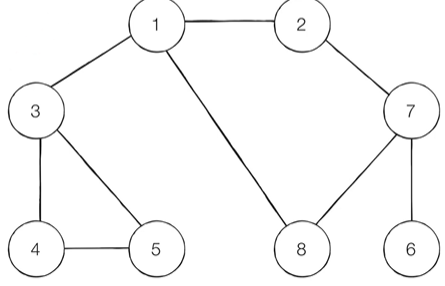
- 큐에서 노드 1을 꺼내, 방문 하지 않은 2, 3, 8을 큐에 삽입하고 방문 처리 ! ( 작은 수 부터 )
- 큐에서 노드 2를 꺼내, 방문 하지 않은 7를 큐에 삽입하고 방문 처리 !
- 큐에서 노드 3을 꺼내, 방문 하지 않은 4, 5를 큐에 삽입하고 방문 처리 !
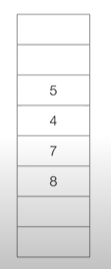
- 큐에서 노드 8을 꺼내, 방문 하지 않은게 없네!! 무시 !
=> 1, 2, 3, 8, 7, 4, 5, 6 ( 전체 노드 탐색 순서, 큐에 들어간 순서 )
- python
from collections import deque
def bfs(graph, start, visited) :
queue = deque([start])
# 현재 노드를 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue :
v = queue.popleft()
print(v, end = " ")
# 아직 방문하지 않은 인접 원소를 큐에 삽입
for i in graph[v] :
if not visited[i] :
queue.append(i)
visited[i] = True
# 각 노드가 연결된 정보 표현 ( 2차원 리스트 )
graph = [
[],
[2, 3, 5],
[1, 7],
[1, 4, 5],
[3, 4],
[3, 5],
[2, 5, 4],
[7],
[1, 7]
]
# 각 노드가 방문된 정보 표현 ( 1차원 리스트 )
visited = [False] * 9
dfs(graph, 1, visited)
# result
# 1 2 7 3 4 5- c++
#include <bits/stdc++.h>
using namespace std;
bool visited[9];
vector<int> graph[9];
// BFS 함수 정의
void bfs(int start) {
queue<int> q;
q.push(start);
// 현재 노드를 방문 처리
visited[start] = true;
// 큐가 빌 때까지 반복
while(!q.empty()) {
// 큐에서 하나의 원소를 뽑아 출력
int x = q.front();
q.pop();
cout << x << ' ';
// 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for(int i = 0; i < graph[x].size(); i++) {
int y = graph[x][i];
if(!visited[y]) {
q.push(y);
visited[y] = true;
}
}
}
}
int main(void) {
// 노드 1에 연결된 노드 정보 저장
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
// 노드 2에 연결된 노드 정보 저장
graph[2].push_back(1);
graph[2].push_back(7);
// 노드 3에 연결된 노드 정보 저장
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
// 노드 4에 연결된 노드 정보 저장
graph[4].push_back(3);
graph[4].push_back(5);
// 노드 5에 연결된 노드 정보 저장
graph[5].push_back(3);
graph[5].push_back(4);
// 노드 6에 연결된 노드 정보 저장
graph[6].push_back(7);
// 노드 7에 연결된 노드 정보 저장
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
// 노드 8에 연결된 노드 정보 저장
graph[8].push_back(1);
graph[8].push_back(7);
bfs(1);
}- java
import java.util.*;
public class Main {
public static boolean[] visited = new boolean[9];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// BFS 함수 정의
public static void bfs(int start) {
Queue<Integer> q = new LinkedList<>();
q.offer(start);
// 현재 노드를 방문 처리
visited[start] = true;
// 큐가 빌 때까지 반복
while(!q.isEmpty()) {
// 큐에서 하나의 원소를 뽑아 출력
int x = q.poll();
System.out.print(x + " ");
// 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for(int i = 0; i < graph.get(x).size(); i++) {
int y = graph.get(x).get(i);
if(!visited[y]) {
q.offer(y);
visited[y] = true;
}
}
}
}
public static void main(String[] args) {
// 그래프 초기화
for (int i = 0; i < 9; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(1).add(8);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(1);
graph.get(2).add(7);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(1);
graph.get(3).add(4);
graph.get(3).add(5);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
graph.get(4).add(5);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(3);
graph.get(5).add(4);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(7);
// 노드 7에 연결된 노드 정보 저장
graph.get(7).add(2);
graph.get(7).add(6);
graph.get(7).add(8);
// 노드 8에 연결된 노드 정보 저장
graph.get(8).add(1);
graph.get(8).add(7);
bfs(1);
}
}
728x90
반응형
'🦥 코테 > 이것이 코딩 테스트다 with python' 카테고리의 다른 글
| [이것이 코딩 테스트다 with Python]_21_선택정렬 (0) | 2022.02.08 |
|---|---|
| [이것이 코딩 테스트다 with Python]_20_DFS & BFS 문제풀이 (0) | 2022.02.02 |
| [이것이 코딩 테스트다 with Python]_18_DFS (0) | 2022.02.02 |
| [이것이 코딩 테스트다 with Python]_17_재귀 함수 (0) | 2022.02.02 |
| [이것이 코딩 테스트다 with Python]_16_스택과 큐 (0) | 2022.02.02 |
Comments




