😎 공부하는 징징알파카는 처음이지?
[이것이 코딩 테스트다 with Python]_28_다이나믹 프로그래밍 본문
220209 작성
<본 블로그는 『이것이 취업을 위한 코딩 테스트다』 의 youtube를 참고해서 공부하며 작성하였습니다>
https://www.youtube.com/watch?v=rWbjQphRE9A&list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81&index=28
1. 다이나믹 프로그래밍
: 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상
: 이미 계산된 결과 (작은 문제)는 별도의 메모리 영역에 저장 (다시 계산 X)
: 두 가지 탑다운(위에서 아래, 하향식 ), 보텀업(아래에서 위, 상향식)으로 구성
: 동적 계획법
: 자료구조에서 동적 할당은 프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법
=> 다이나믹은 별다른 의미 없이 사용
1. 최적 부분 구조 (Optimal Substructure)
: 큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아 큰 문제 해결
2. 중복되는 부분 문제 (Overlapping Subproblem)
: 동일한 작은 문제를 반복적으로 해결
2. 피보나치 수열
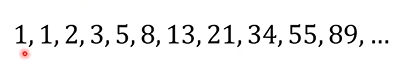
: 점화식이란 인접한 항들 사이의 관계식
: 배열이나 리스트 이용
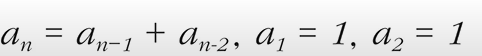
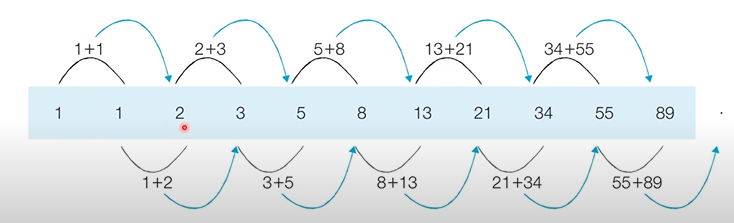
+) 단순 재귀 함수는 지수 시간 복잡도 가진다
: 여러번 호출, 중복되는 부분!!
- python
# 재귀 함수 구현
def fibo(x) :
if x == 1 or x == 2 :
return 1
return fibo(x-1) + fibo(x-2)
print(fibo(6))- c++
#include <bits/stdc++.h>
using namespace std;
// 피보나치 함수(Fibonacci Function)을 재귀함수로 구현
int fibo(int x) {
if (x == 1 || x == 2) {
return 1;
}
return fibo(x - 1) + fibo(x - 2);
}
int main(void) {
cout << fibo(4) << '\n';
}- java
import java.util.*;
public class Main {
// 피보나치 함수(Fibonacci Function)을 재귀함수로 구현
public static int fibo(int x) {
if (x == 1 || x == 2) {
return 1;
}
return fibo(x - 1) + fibo(x - 2);
}
public static void main(String[] args) {
System.out.println(fibo(4));
}
}
3. 피보나치 수열 시간 복잡도
: 세타 표기법 - θ(1.618....^N)
: 빅오 표기법 - O(2^N)
4. 메모이제이션 (Memoization)
: 다이나믹 프로그래밍 구현 방법
: 한 번 계산한 결과를 메모리 공간에 메모
: 같은 문제 다시 호출하면, 메모한 결과 가져옴
: 값 기록하기 = 캐싱 (cashing)
: 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념
: 다이나믹 프로그래밍에 국한되지 X
5. 탑다운 vs 보텀업
- 탑다운 (메모이제이션)
: 하향식
- 보텀업
: 상향식
: 다이나믹 프로그래밍의 전형적인 형태
: 결과 저장용 리스트는 DP 테이블
+) 탑다운 다이나믹 프로그래밍
- python
# 메모이제이션 d = [0] * 100 def fibo(x) : if x == 1 or x ==2 : return 1 # 이미 계산 if d[x] !=0 : return d[x] # 아직 계산 x d[x] = fibo(x - 1) + fibo(x - 2) return d[x] print(fibo(99))

- c++
#include <bits/stdc++.h>
using namespace std;
// 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 배열 초기화
long long d[100];
// 피보나치 함수(Fibonacci Function)를 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
long long fibo(int x) {
// 종료 조건(1 혹은 2일 때 1을 반환)
if (x == 1 || x == 2) {
return 1;
}
// 이미 계산한 적 있는 문제라면 그대로 반환
if (d[x] != 0) {
return d[x];
}
// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
d[x] = fibo(x - 1) + fibo(x - 2);
return d[x];
}
int main(void) {
cout << fibo(50) << '\n';
}
- java
import java.util.*;
public class Main {
// 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 배열 초기화
public static long[] d = new long[100];
// 피보나치 함수(Fibonacci Function)를 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
public static long fibo(int x) {
// 종료 조건(1 혹은 2일 때 1을 반환)
if (x == 1 || x == 2) {
return 1;
}
// 이미 계산한 적 있는 문제라면 그대로 반환
if (d[x] != 0) {
return d[x];
}
// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
d[x] = fibo(x - 1) + fibo(x - 2);
return d[x];
}
public static void main(String[] args) {
System.out.println(fibo(50));
}
}
+) 보텀업 다이나믹 프로그래밍
- python
d = [0]*100
d[1] = 1
d[2] = 1
n = 99
for i in range(3, n+1) :
d[i] = d[i-1] + d[i-2]
print(d[n])
- c++
#include <bits/stdc++.h>
using namespace std;
// 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
long long d[100];
int main(void) {
// 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1;
d[2] = 1;
int n = 50; // 50번째 피보나치 수를 계산
// 피보나치 함수(Fibonacci Function) 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for (int i = 3; i <= n; i++) {
d[i] = d[i - 1] + d[i - 2];
}
cout << d[n] << '\n';
}- java
import java.util.*;
public class Main {
public static long[] d = new long[100];
public static void main(String[] args) {
// 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1;
d[2] = 1;
int n = 50; // 50번째 피보나치 수를 계산
// 피보나치 함수(Fibonacci Function) 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for (int i = 3; i <= n; i++) {
d[i] = d[i - 1] + d[i - 2];
}
System.out.println(d[n]);
}
}
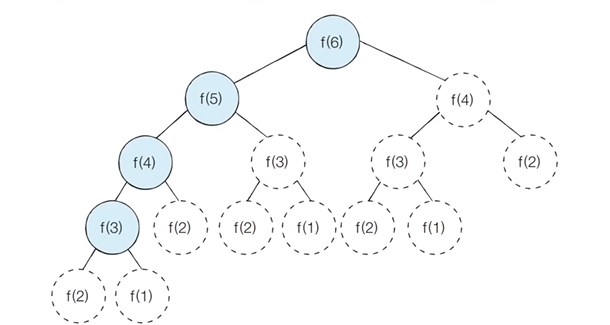
+) 피보나치 수열 : 메모이제이션 동작 분석
: 이미 계산된 결과는 메모리에 저장
: 메모이제이션 이용하면 피보나치 수열 시간 복잡도는 O(N)
- python
d = [0] * 100
def fibo(x) :
print("f(" + str(x) + ")", end = " ")
if x == 1 or x == 2 :
return 1
if d[x] != 0 :
return d[x]
d[x] = fibo(x - 1) + fibo(x - 2)
return d[x]
fibo(6)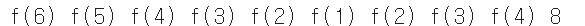
6. 다이나믹 프로그래밍 VS 분할 정복
: 모두 최적 부분 구조 가질 때 사용
( 큰 문제를 작은 문제로 나누고, 작은 문제의 답을 모아서 큰 문제 해결)
: 차이점은 부분 문제의 중복
( 다이나믹은 각 부분 문제들이 서로 영향 미치며 부분 문제 중복)
( 분할 정복에서는 동일한 부분 문제가 반복적 계산 X)
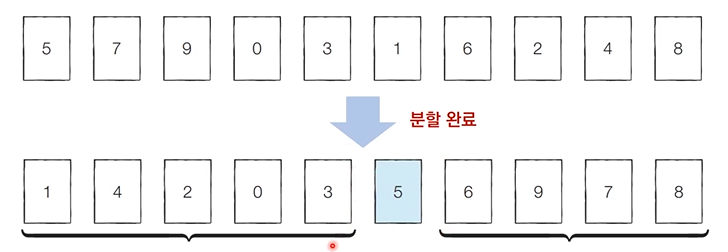
EX) 분할 정복 예시 퀵 정렬
: 기준 원소 PIVOT 이 자리를 변경해서 자리 잡으면, 그 기준 원소의 위치는 바뀌지 않음
7. 다이나믹 프로그래밍 접근
: 다이나믹 프로그래밍 유형 파악
: 그리디, 구현, 완전 탐색인가
: 재귀로 비효율적인 완전 탐색 프로그램 작성 -> 탑다운 문제 사용
'🦥 코테 > 이것이 코딩 테스트다 with python' 카테고리의 다른 글
| [이것이 코딩 테스트다 with Python]_30_다익스트라 최단 경로 알고리즘 (0) | 2022.02.12 |
|---|---|
| [이것이 코딩 테스트다 with Python]_29_다이나믹 프로그래밍 기초 문제 풀이 (0) | 2022.02.11 |
| [이것이 코딩 테스트다 with Python]_27_이진 탐색 문제풀이 (0) | 2022.02.09 |
| [이것이 코딩 테스트다 with Python]_26_이진탐색 (0) | 2022.02.08 |
| [이것이 코딩 테스트다 with Python]_25_정렬 알고리즘 비교 & 문제 풀이 (0) | 2022.02.08 |




