😎 공부하는 징징알파카는 처음이지?
[이것이 코딩 테스트다 with Python]_32_최단 경로 알고리즘 기초 문제 풀이 본문
🦥 코테/이것이 코딩 테스트다 with python
[이것이 코딩 테스트다 with Python]_32_최단 경로 알고리즘 기초 문제 풀이
징징알파카 2022. 2. 13. 00:01728x90
반응형
220213 작성
<본 블로그는 『이것이 취업을 위한 코딩 테스트다』 의 youtube를 참고해서 공부하며 작성하였습니다>
https://www.youtube.com/watch?v=liuUazQaLuU&list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81&index=32
< 문제1 > 전보
: N 개의 도시가 있다
: 각 도시의 번호와 통로가 설치되어 있는 정보가 주어졌을 때, 도시 C 에서 보낸 메시지를 받게 되는 도시의 개수는 몇개, 도시들이 모두 메시지를 받는 데까지 걸리는 시간은 얼마인가
: 한 도시에서 다른 도시까지의 최단 거리 문제로 치환
: 우선순위 큐(HEAP)를 이용한 다익스트라 알고리즘
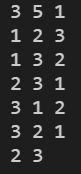
- python
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수, 간선의 개수, 시작 노드를 입력받기
n, m, start = map(int, input().split())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
# 모든 간선 정보를 입력받기
for _ in range(m):
x, y, z = map(int, input().split())
# X번 노드에서 Y번 노드로 가는 비용이 Z라는 의미
graph[x].append((y, z))
def dijkstra(start):
q = []
# 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q: # 큐가 비어있지 않다면
# 가장 최단 거리가 짧은 노드에 대한 정보를 꺼내기
dist, now = heapq.heappop(q)
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
cost = dist + i[1]
# 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
# 다익스트라 알고리즘을 수행
dijkstra(start)
# 도달할 수 있는 노드의 개수
count = 0
# 도달할 수 있는 노드 중에서, 가장 멀리 있는 노드와의 최단 거리
max_distance = 0
for d in distance:
# 도달할 수 있는 노드인 경우
if d != 1e9:
count += 1
max_distance = max(max_distance, d)
# 시작 노드는 제외해야 하므로 count - 1을 출력
print(count - 1, max_distance)
- c++
#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
using namespace std;
// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
vector<pair<int, int> > graph[30001];
// 최단 거리 테이블 만들기
int d[30001];
void dijkstra(int start) {
priority_queue<pair<int, int> > pq;
// 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
pq.push({0, start});
d[start] = 0;
while (!pq.empty()) { // 큐가 비어있지 않다면
// 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
int dist = -pq.top().first; // 현재 노드까지의 비용
int now = pq.top().second; // 현재 노드
pq.pop();
// 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if (d[now] < dist) continue;
// 현재 노드와 연결된 다른 인접한 노드들을 확인
for (int i = 0; i < graph[now].size(); i++) {
int cost = dist + graph[now][i].second;
// 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if (cost < d[graph[now][i].first]) {
d[graph[now][i].first] = cost;
pq.push(make_pair(-cost, graph[now][i].first));
}
}
}
}
int main(void) {
cin >> n >> m >> start;
// 모든 간선 정보를 입력받기
for (int i = 0; i < m; i++) {
int x, y, z;
cin >> x >> y >> z;
// X번 노드에서 Y번 노드로 가는 비용이 Z라는 의미
graph[x].push_back({y, z});
}
// 최단 거리 테이블을 모두 무한으로 초기화
fill(d, d + 30001, INF);
// 다익스트라 알고리즘을 수행
dijkstra(start);
// 도달할 수 있는 노드의 개수
int count = 0;
// 도달할 수 있는 노드 중에서, 가장 멀리 있는 노드와의 최단 거리
int maxDistance = 0;
for (int i = 1; i <= n; i++) {
// 도달할 수 있는 노드인 경우
if (d[i] != INF) {
count += 1;
maxDistance = max(maxDistance, d[i]);
}
}
// 시작 노드는 제외해야 하므로 count - 1을 출력
cout << count - 1 << ' ' << maxDistance << '\n';
}- java
import java.util.*;
class Node implements Comparable<Node> {
private int index;
private int distance;
public Node(int index, int distance) {
this.index = index;
this.distance = distance;
}
public int getIndex() {
return this.index;
}
public int getDistance() {
return this.distance;
}
// 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
@Override
public int compareTo(Node other) {
if (this.distance < other.distance) {
return -1;
}
return 1;
}
}
public class Main {
public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정
// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
public static int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
// 최단 거리 테이블 만들기
public static int[] d = new int[30001];
public static void dijkstra(int start) {
PriorityQueue<Node> pq = new PriorityQueue<>();
// 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
pq.offer(new Node(start, 0));
d[start] = 0;
while(!pq.isEmpty()) { // 큐가 비어있지 않다면
// 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
Node node = pq.poll();
int dist = node.getDistance(); // 현재 노드까지의 비용
int now = node.getIndex(); // 현재 노드
// 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if (d[now] < dist) continue;
// 현재 노드와 연결된 다른 인접한 노드들을 확인
for (int i = 0; i < graph.get(now).size(); i++) {
int cost = d[now] + graph.get(now).get(i).getDistance();
// 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if (cost < d[graph.get(now).get(i).getIndex()]) {
d[graph.get(now).get(i).getIndex()] = cost;
pq.offer(new Node(graph.get(now).get(i).getIndex(), cost));
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
start = sc.nextInt();
// 그래프 초기화
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<Node>());
}
// 모든 간선 정보를 입력받기
for (int i = 0; i < m; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
// X번 노드에서 Y번 노드로 가는 비용이 Z라는 의미
graph.get(x).add(new Node(y, z));
}
// 최단 거리 테이블을 모두 무한으로 초기화
Arrays.fill(d, INF);
// 다익스트라 알고리즘을 수행
dijkstra(start);
// 도달할 수 있는 노드의 개수
int count = 0;
// 도달할 수 있는 노드 중에서, 가장 멀리 있는 노드와의 최단 거리
int maxDistance = 0;
for (int i = 1; i <= n; i++) {
// 도달할 수 있는 노드인 경우
if (d[i] != INF) {
count += 1;
maxDistance = Math.max(maxDistance, d[i]);
}
}
// 시작 노드는 제외해야 하므로 count - 1을 출력
System.out.println((count - 1) + " " + maxDistance);
}
}
< 문제2 > 미래 도시
: 1번 부터 N 번까지의 회사가 있는데 특정 회사끼리는 서로 도로를 통해 연결
: 연결된 2개의 회사는 양방향으로 이동 가능
: 판매원 A는 1번 회사에서 출발하여 K 회사로 가는 최소 이동시간을 출력
=> 전형적인 최단 거리 문제
=> 플로이드 워셜 알고리즘 수행후 1번 노드에서 X 까지의 최단 거리 + X 에서 K 까지의 최단 거리 계산하여 출력
- python
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수 및 간선의 개수를 입력받기
n, m = map(int, input().split())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
for b in range(1, n + 1):
if a == b:
graph[a][b] = 0
# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
# A와 B가 서로에게 가는 비용은 1이라고 설정
a, b = map(int, input().split())
graph[a][b] = 1
graph[b][a] = 1
# 거쳐 갈 노드 X와 최종 목적지 노드 K를 입력받기
x, k = map(int, input().split())
# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 수행된 결과를 출력
distance = graph[1][k] + graph[k][x]
# 도달할 수 없는 경우, -1을 출력
if distance >= 1e9:
print("-1")
# 도달할 수 있다면, 최단 거리를 출력
else:
print(distance)
- c++
#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
using namespace std;
// 노드의 개수(N), 간선의 개수(M)
int n, m;
// 2차원 배열(그래프 표현)를 만들기
int graph[101][101];
int main(void) {
cin >> n >> m;
// 최단 거리 테이블을 모두 무한으로 초기화
for (int i = 0; i < 101; i++) {
fill(graph[i], graph[i] + 101, INF);
}
// 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
if (a == b) graph[a][b] = 0;
}
}
// 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for (int i = 0; i < m; i++) {
// A와 B가 서로에게 가는 비용은 1이라고 설정
int a, b;
cin >> a >> b;
graph[a][b] = 1;
graph[b][a] = 1;
}
// 거쳐 갈 노드 X와 최종 목적지 노드 K를 입력받기
int x, k;
cin >> x >> k;
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for (int k = 1; k <= n; k++) {
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// 수행된 결과를 출력
int distance = graph[1][k] + graph[k][x];
// 도달할 수 없는 경우, -1을 출력
if (distance >= INF) {
cout << "-1" << '\n';
}
// 도달할 수 있다면, 최단 거리를 출력
else {
cout << distance << '\n';
}
}- java
import java.util.*;
public class Main {
public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정
// 노드의 개수(N), 간선의 개수(M), 거쳐 갈 노드(X), 최종 목적지 노드(K)
public static int n, m, x, k;
// 2차원 배열(그래프 표현)를 만들기
public static int[][] graph = new int[101][101];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
// 최단 거리 테이블을 모두 무한으로 초기화
for (int i = 0; i < 101; i++) {
Arrays.fill(graph[i], INF);
}
// 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
if (a == b) graph[a][b] = 0;
}
}
// 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for (int i = 0; i < m; i++) {
// A와 B가 서로에게 가는 비용은 1이라고 설정
int a = sc.nextInt();
int b = sc.nextInt();
graph[a][b] = 1;
graph[b][a] = 1;
}
x = sc.nextInt();
k = sc.nextInt();
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for (int k = 1; k <= n; k++) {
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// 수행된 결과를 출력
int distance = graph[1][k] + graph[k][x];
// 도달할 수 없는 경우, -1을 출력
if (distance >= INF) {
System.out.println(-1);
}
// 도달할 수 있다면, 최단 거리를 출력
else {
System.out.println(distance);
}
}
}
728x90
반응형
'🦥 코테 > 이것이 코딩 테스트다 with python' 카테고리의 다른 글
| [이것이 코딩 테스트다 with Python]_34_서로소 집합을 활용한 사이클 판별 (0) | 2022.02.13 |
|---|---|
| [이것이 코딩 테스트다 with Python]_33_서로소 집합 자료구조 (0) | 2022.02.13 |
| [이것이 코딩 테스트다 with Python]_31_ 플로이드 워셜 알고리즘 (0) | 2022.02.12 |
| [이것이 코딩 테스트다 with Python]_30_다익스트라 최단 경로 알고리즘 (0) | 2022.02.12 |
| [이것이 코딩 테스트다 with Python]_29_다이나믹 프로그래밍 기초 문제 풀이 (0) | 2022.02.11 |
Comments




